Research projects
Impurities on superconductors
Systems of interest: magnetic impurities (atoms, molecules) deposited on the surface of a conventional (BCS) superconductor
Methods: dynamical mean-field theory, quantum Monte Carlo, diagrammatic perturbation techniques
Goal: explain the interplay between the superconducting order and the magnetic moment in two-dimensional layered systemsRelated publications
C. Li, V. Pokorný, M. Žonda, J.-C. Liu, P. Zhou, O. Chahib, T. Glatzel, R. Häner, S. Decurtins,
S.-X. Liu, R. Pawlak, E. Meyer, arxiv:2408.05115 (2024).
V. Pokorný and P. Ram, Phys. Rev. B 104, 155102 (2021). (pdf)Presentations
6. 2. 2024, FZU - Institute of Physics, Czech Academy of Scences, Prague
28. 6. 2021, Superconducting Hybrids @ Extreme, Štrbské Pleso, Slovakia
Superconducting quantum dots
Systems of interest: single-level quantum dots with local Coulomb interaction connected to metallic and superconducting (BCS) leads that can be described by the superconducting impurity Anderson model
Methods: second order perturbation theory in Coulomb interaction stregth, numerical renormalization group (NRG), CT-HYB quantum Monte Carlo
Goal: consistent description of the behavior of the subgap Andreev bound states (Yu-Shiba-Rusinov states) and the Josephson current in the vicinity of the single-doublet (zero-pi) quantum phase transitionRelated publications
V. Pokorný and M. Žonda, Phys. Rev. B 107, 155111 (2023). (pdf)
M. Žonda, P. Zalom, T. Novotný, G. Loukeris, J. Bätge, and V. Pokorný,
Phys. Rev. B 107, 115407 (2023). (pdf)
V. Pokorný and T. Novotný, Phys. Rev. Research 3, 023013 (2021). (pdf)
P. Zalom, V. Pokorný, and T. Novotný, Phys. Rev. B 103, 035419 (2021). (pdf)
V. Pokorný, M. Žonda, G. Loukeris, and T. Novotný, JPS Conf. Proc. 30, 011002 (2020).
A. Kadlecová, M. Žonda, V. Pokorný, and T. Novotný,
Phys. Rev. Applied 11, 044094 (2019). (pdf)
V. Pokorný, M. Žonda, Physica B 536, 488 (2018).
T. Domański, M. Žonda, V. Pokorný, G. Górski, V. Janiš, and T. Novotný,
Phys. Rev. B 95, 045104 (2017). (pdf)
V. Janiš, V. Pokorný, and M. Žonda, Eur. Phys. J. B 89, 197 (2016).
M. Žonda, V. Pokorný, V. Janiš, and T. Novotný, Phys. Rev. B 93, 024523 (2016). (pdf)
M. Žonda, V. Pokorný, V. Janiš, and T. Novotný, Sci. Rep. 5, 8821 (2015).
Presentations
13. 12. 2022, FZU - Institute of Physics, Czech Academy of Scences, Prague
18. 6. 2019, FZU - Institute of Physics, Czech Academy of Scences,Prague
12. 3. 2018, DPG Spring Meeting, Berlin, Germany
1. 1. 2018, Universität Regensburg, Germany
24. 3. 2015, FZU - Institute of Physics, Czech Academy of Scences, Prague
17. 10. 2014, IIASS, Vietri sul Mare (Salerno), ItalySoftware
SQUAD - SUperconducting QUAntum Dot - set of python scripts to calculate properties of these systems using the diagrammatic second order perturbation method
Molecular electronics
Systems of interest: spinful molecules attached to metallic or insulating substrates or leads
Methods: density functional theory (DFT), non-equilibrium Green functions (NEGF)
Goal: search for molecular systems suitable as building elements of molecular spintronic devicesRelated publications
H. Li et al, Angew. Chem. Int. Ed. 56 14145 (2017).Presentations
17. 2. 2020, Albert-Ludwigs-Universität Freiburg, Germany
2. 7. 2019, Prague, Czech Republic
20. 7. 2018, Universität Regensburg, Germany
Thermodynamically consistent description of quantum criticality
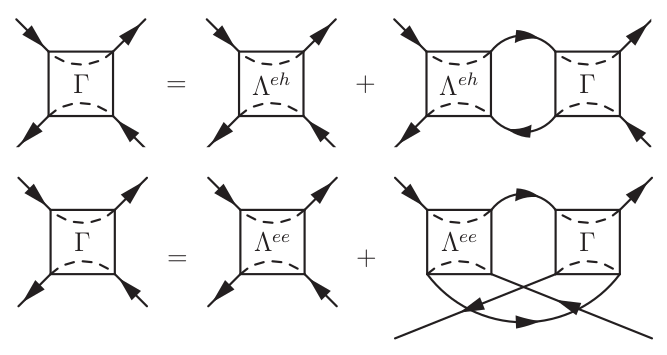
Systems of interest: lattice models of correlated electrons: Anderson and Hubbard model
Methods: one- and two-particle Green functions, simplified parquet equations
Goal: to develop consistent methods based on advanced diagrammatic perturbation techniques to study quantum criticality in interacting electron systemsRelated publications
V. Janiš, V. Pokorný, Š. Kos, Phys. Rev. B 109, 075171 (2024). (pdf)
V. Janiš, A. Klíč, J. Yan, and V. Pokorný, Phys. Rev. B 102, 205120 (2020). (pdf)
V. Janiš, P. Zalom, V. Pokorný, and A. Klíč, Phys. Rev. B 100, 195114 (2019). (pdf)
V. Janiš, V. Pokorný, and A. Kauch, Phys. Rev. B 95, 165113 (2017). (pdf)
V. Janiš, A. Kauch, and V. Pokorný, Phys. Rev. B 95, 045108 (2017). (pdf)
Presentations
Poster from the 2017 summer school in Tallahassee (pdf)Software
SPEpy - Simplified Parquet Equations in python - set of python scripts to calculate properties of the single-impurity Anderson model using the simplified parquet equation solverCorrelated materials with strong spin-orbit interactions
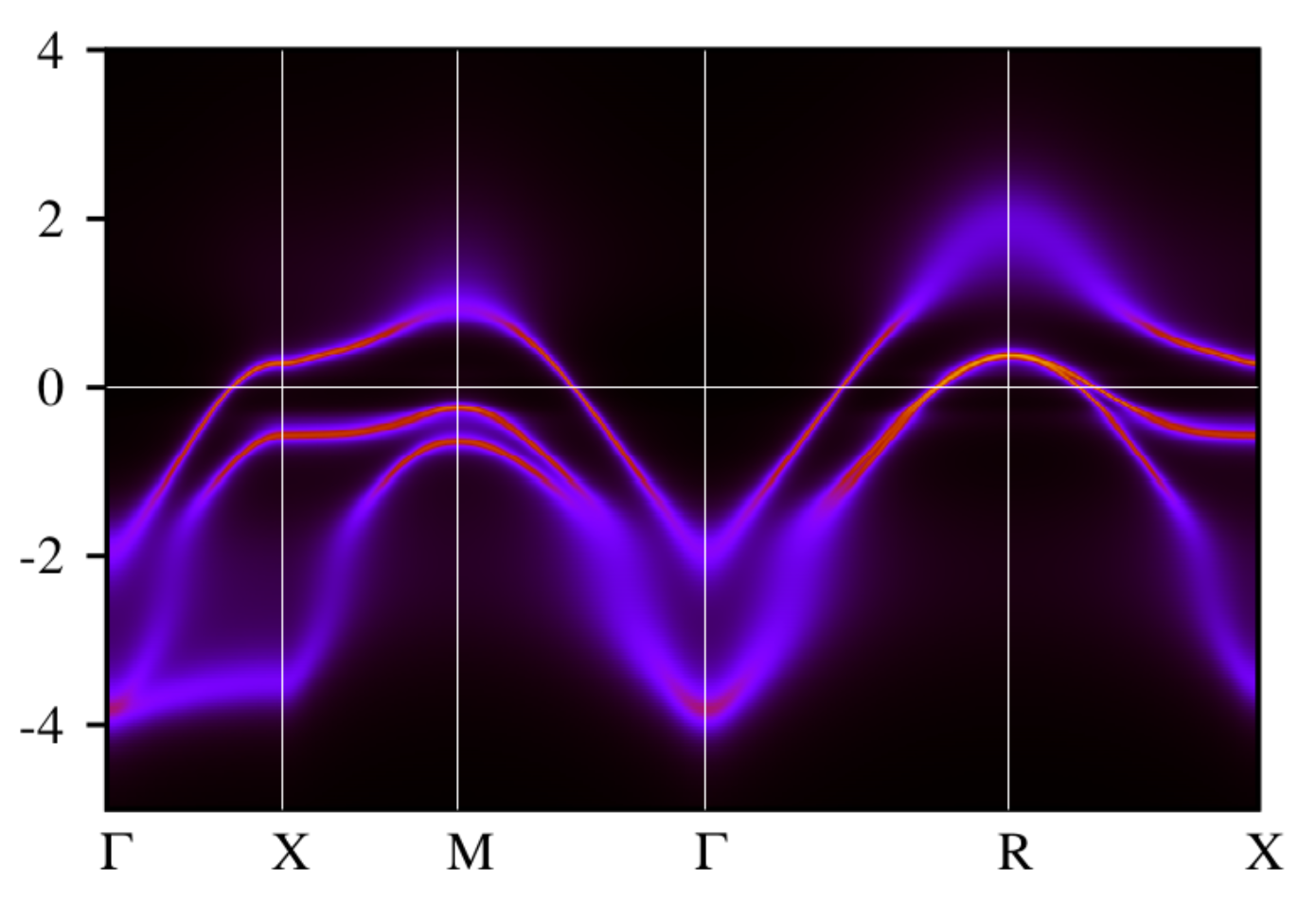
Systems of interest: transition metal oxides with strong spin-orbit coupling, multi-band Hubbard model
Methods: density functional theory, dynamical mean-dield theory, quantum Monte Carlo
Goal: calculate spectral, transport and magnetic properties of novel materials based on transition metal oxidesRelated publications
K. Pajskr, P. Novák, V. Pokorný, J. Kolorenč, R. Arita, and J. Kuneš,
Phys. Rev. B 93, 035129 (2016). (pdf)Correlated electrons in disordered alloys (PhD thesis)
We developed methods to calculate charge transport in disordered systems of elastically scattered electrons. These diagrammatic methods are based on an asymptotic limit to high spatial dimensions and utilize advanced diagram summation techniques on the two-particle level. They allow us to calculate electrical conductivity and diffusion coefficient for arbitrary disorder strength. The numerical calculations are performed on the disordered Anderson model and the Falicov-Kimball model.
Related publications
V. Janiš and V. Pokorný, Phys. Rev. B 90, 045143 (2014). (pdf)
V. Pokorný and V. Janiš, J. Phys.: Cond. Mat. 25, 175502 (2013).
V. Janiš and V. Pokorný, Ann. Phys. (Berlin) 523, 715 (2011).
V. Janiš and V. Pokorný, Phys. Rev. B 81, 165103 (2010). (pdf)
PhD thesis (English, pdf, defended in 2013 at Charles University in Prague).Presentations
24. 4. 2012, FZU - Institute of Physics, Czech Academy of Scences, Prague
14. 10. 2011, IIASS, Vietri sul Mare (Salerno), Italy
Critical properties of the mixed-spin Heisenberg model (Master thesis)
We studied the critical properties of the anisotropic mixed spin-1 and spin-1/2 quantum Heisenberg model using a simple two-site mean-field approximation. We treat in detail the system on the simple cubic lattice considering both exchange anisotropy and uniaxial singe-ion anisotropy. The critical behavior is analysed and the complete phase diagrams were calculated, where aside from the typical ferromagnetic phase a low-temperature quantum ordered phase is described.
Related publications
A. Bobák, V. Pokorný, and J. Dely, J. Phys.: Conf. Ser. 200, 022001 (2010).
A. Bobák, V. Pokorný, and J. Dely, Physica A 388, 2157 (2009).
Master thesis (Slovak, pdf, defended in 2008 at Pavol Jozef Šafárik University in Košice).Presentations
16. 12. 2008, FZU - Institute of Physics, Czech Academy of Scences, Prague